목차
열역학을 공부하다보면 PV 그래프를 접하게 된다.
이상기체의 PV 그래프에 대해서 내가 알고 있는 것들을 간단하게 정리해보려고 한다.
기본 설명
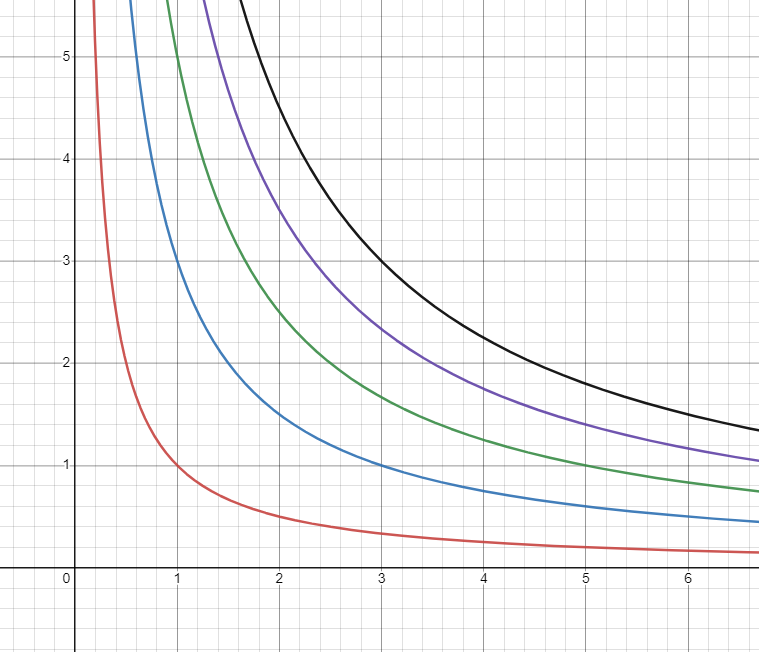
PV그래프는 기본적으로 P(압력), V(부피), T(온도) 세 변수로 그려지는 3차원 그래프를 T가 등위인 등위선으로 PV평면에 그린 것이다.
다른 변수로 등위선을 그리면 부피 온도 그래프 혹은 압력 온도 그래프를 그릴 수 있다.
\[\begin{gather} PV=Nk_bT \\ \text{혹은} \\ PV=nRT \end{gather}\]이러한 이상기체 상태방정식 (Ideal Gas Law)에서 기체분자의 수는 고정이라고 했을 때, T에 대한 등위선을 그리게 되면 각 T마다 nRT가 상수가 되어 PV가 반비례 관계가 되는 것을 볼 수 있다.
이러한 선을 이 글에서는 등온선이라고 하겠다.
또한, 위에 있는 공식에서 잘 생각해보면, 기체의 양이 변하지 않을 때 어떠한 한 지점(p,v) 에서 P축과 V축에 각각 수선의 발을 그었을 때, PV축과 수선의 발들로 이루어진 직사각형의 크기가 온도의 척도가 된다는 것을 알 수 있다.
이 것은 원점에 가까운 등온선일 수록 온도가 낮다는 것을 의미한다.
이와 같은 방법으로 V를 고정시키면 P랑 T가 비례하게 되고, P를 고정시키면 V와 T가 비례하게 된다.
즉, P나 V가 고정되었을 때는 일차함수로 그려진다.
이상기체에서의 압력(P)는 기체분자들이 얼마나 자주 벽과 충돌하는지와 관련이 있다.
더 자주 그리고 더 빠르게 충돌할수록 충격량과 벽에 가하는 힘이 더 클 것이고, 당연히 단위면적당 가해지는 힘(압력)도 높을 것이다.
기체의 온도(~ 속도)와 높을 수록, 기체의 양이 많아질수록 압력과 충돌 횟수는 증가한다.
PV그래프로 돌아와서, PV그래프 상에서 움직임이 생긴다면, 그것은 움직임 과정 중에 에너지가 변했다는 뜻이다.
등온과정에서도 최종 에너지의 변화량(∆U)은 0이지만 중간에 움직임에는 에너지의 변화가 개입할 수 밖에 없다.
예를 들어 같은 높이에서 같은 위치에너지를 가지더라도, 수평이동을 하면 에너지의 변화가 발생했었을 수 밖에 없는 것이랑 같다.
기본 공식들
여기서의 W와 Q는 기체에게 가해진 에너지(기체가 얻은 에너지)이라는 전제하에 글을 쓰도록 하겠다.
\[\begin{align} & PV = nRT = Nk_bT \tag{1} \\ & \overline K = \frac{3}{2} k_bT \tag{2} \\ & \Delta \overline{K} = \frac{3}{2} k_B \Delta T \tag{3} \\ & \Delta U = W + Q \tag{4} \\ \end{align}\]PV 그래프의 해석
등온과정
등온과정은 기체의 온도가 변하지 않는 과정이다.
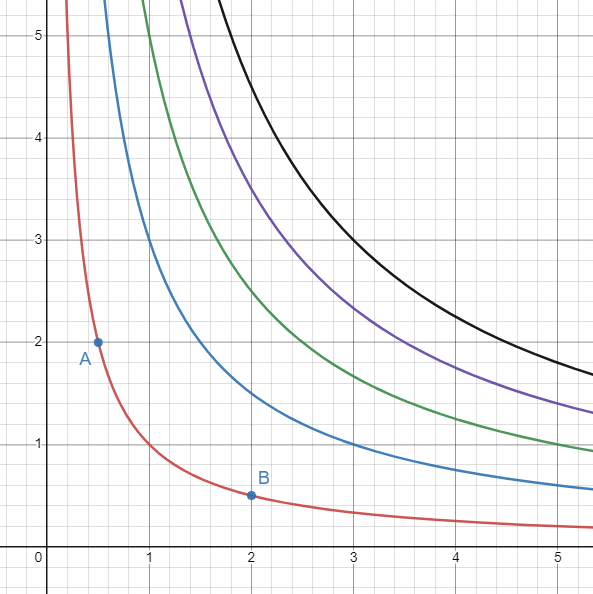
PV 그래프에서는 등온선을 따라 이동하는 과정이 등온과정이다.
예를 들어 위 예시에서 A에서 B로, 혹은 그 반대가 등온 과정의 예시이다.A에서 B의 과정을 보자면, 기체에 가해진 일(W)이 negative이기 때문에 (기체가 용기에 일(W)을 해서 부피가 팽창했기 때문에), 내부 기체가 운동량을 잃었음으로 그 만큼의 에너지를 열량(Q)에서 얻어와야 등온과정이 성립한다.
정리해보자면, 등온과정의 특징으로는 기체의 에너지의 변화량(∆U)이 0이라는 점과, 기체에 가해진 일(W)과 기체가 얻은 열량(Q)은 크기가 같고, 부호만 서로 반대라는 점이다.
\[\begin{align} &\Delta U = 0 \\ & Q = -W \end{align}\]5번 식을 3번 식에 대입하여 6번 식을 얻어낼 수 있다.
등적과정
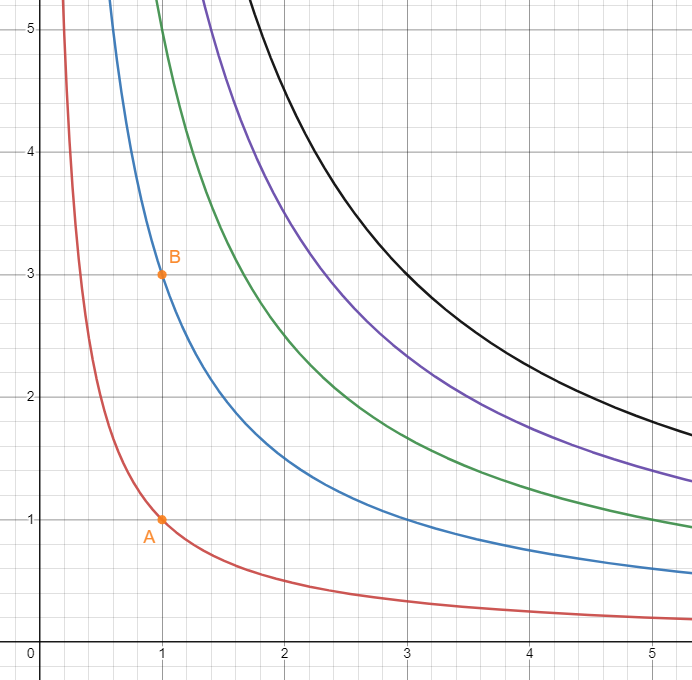
등적과정은 기체의 부피가 변하지 않는 과정이다.
위 그림에서 A에서 B의 과정 혹은 그 반대가 등적과정의 예시이다.
이 경우, 기체에 가해지는 일(W)이 없기 때문에, 열량(Q)이 에너지의 변화량(∆U)과 동일하다.
\[\begin{align} & W = 0 \tag{5} \\ & \Delta U = Q \tag{6} \end{align}\]온도차를 안다면 그것을 이용해서 기체의 평균 운동에너지의 변화량(∆U)으로 Q를 도출할 수 있다.
다만, 이 경우는 온도가 충분히 낮아서 충분히 낮아 기체 원자들이 바닥상태에 있어야한다.
기체 분자들이 바닥상태에 있다면 아래와 같은 공식을 사용할 수 있다.
\[\begin{align} \Delta E_k = \frac{3}{2} Nk_b \Delta T = \frac{1}{2}m_p(v^2_f - v^2_i) \tag{7} \end{align}\]등압과정
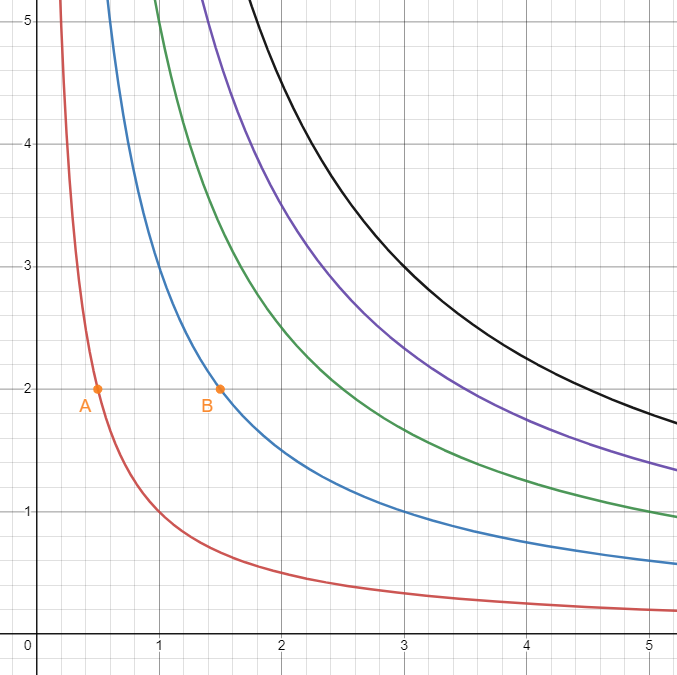
등압과정은 기체의 압력이 변하지 않는 과정이다.
이 경우, 다른 정보가 추가로 주어지지 않는 이상 우리가 아는 것은 오직 기체가 한 일 뿐이다.
기체가 한 일을 구하는 방법은 아래에서 추가로 다루도록 하겠다.
이때 Q는 0이 아니다.
왜냐하면 부피가 변함에도 불구하고 압력을 유지하기 위해서는 기체의 에너지를 증가시켜야하기 때문이다.
단열과정
단열과정은 기체가 얻거나 잃은 열량(Q)이 0일 때이다.
열량이 0이기 때문에 에너지 변화량(∆U)은 기체에 가해진 일(W)과 동일하다.
아래에서 추가로 다루겠지만, 그래프 아래 적분하면 W와 ∆U가 나온다.
\[\begin{align} & Q = 0 \tag{8} \\ & \Delta U = W \tag{9} \end{align}\]PV 그래프 움직임 밑의 영역
PV 그래프에서 어떠한 움직임 과정이 있었다면, 그 움직임 밑의 넓이는 기체에 가해지거나 기체가 한 일이다.
\[\begin{align} W & = Fd = PAd \left(d = \frac{ \Delta V}{A}\right) \tag{10} \\ & = P \bcancel A \frac{ \Delta V}{ \bcancel A} = P \Delta V \tag{11} \end{align}\]이 때, 움직임의 방향은 중요하다.
부피가 팽창했다는 것은 기체에 음의 일(W)이 가해졌다는 뜻이고, 부피가 줄어들었다는 것은 기체에 양의 일(W)이 가해졌다는 뜻이다.
그렇다면 다른 것을 적분하면 열량(Q)가 나올까?
이것에 관해서는 관련 링크를 아래에 올려놓았다.